The Fourier transform of a one-dimensional
aperture (a harbour entrance)
You can find what we derive in this page in any
textbook on optics or Fourier transforms. What you
probably won’t find is the geometrical way I’m going to
derive the result, using my analogy of phase
threads and the mechanical Fourier transform
machine. The result we obtain is exceedingly
important in the wave optics and electron microscopy, for
all sorts of reasons, even though it may seem at first
rather uninteresting.
What we are going to work out is the amplitude
distribution of a plane wave that has passed through a harbour entrance when is arrives in the far-
field Fraunhofer diffraction plane. That is, we want to
work out the Fourier transform of the ‘top hat’ function:
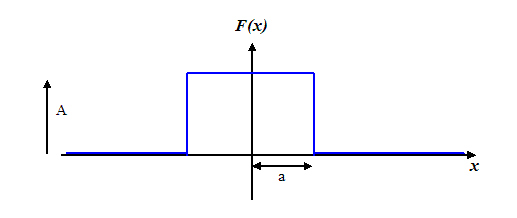
This function is zero everywhere except between x =-a and
x=a, where it has a real value of A. In other words, it
is a harbour wall opening of width 2a with a plane wave
incident upon of modulus A. Because there are no
imaginary parts of the wave, its phase is zero throughout
the whole harbour wall aperture. By putting the function
symmetrically in the middle of the x-axis, then all our
maths is much easier (the Fourier transform is entirely
real – any symmetric real function has a Fourier
transform which is entirely real).
Now, in terms our phase thread analogy, I suggested we
could calculate a Fourier transform using a machine that
looked like this:
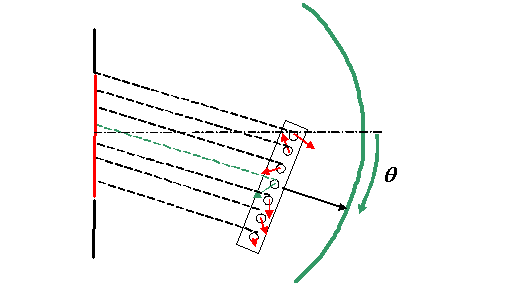 (see previous page)
(see previous page)
As the machine rotates around the green Gaussian surface
(which in practice is very long way from the harbour
entrance), the phase threads pull the little wave value
vectors round and round in the complex plane, via the
pulleys, each of which has a circumference of the
radiation wavelength. The Fourier transform (the
amplitude of the Fraunhofer diffraction pattern) is the
vector addition of all these little wave values.
Well, in the case of our empty one-dimensional aperture
(the harbour wall gap), this process is quite easy to
picture. When θ=0, we have to add up a whole load
of little vectors, all of which are real and of the same
length. I’m going to draw the addition of all these
vectors like this:

The green vector is the wave value emanating from the
centre of the aperture (at x=0): at all values of
θ, this vector stays purely real (pointing to the
right), because no phase difference is introduced to it
as we move the mechanical Fourier transform device around
the Gaussian surface.
At some small value of θ all the red vectors rotate
by a small amount. We add them together as before, tail
to head, and so this ‘snake’ of little vectors begins to
wrap itself up, like this:
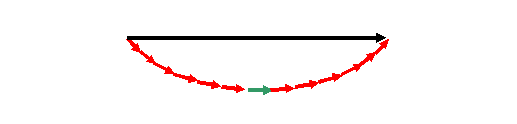
Remember – the green vector stays purely real (pointing
to the right along the real axis of the complex plane).
Vectors further away from the green vector change in
phase quicker (as a function of θ) than those close
to it, because the path length change in their phase
threads is proportional to their distance from x=0. You
see now why it is convenient to define the position of
the aperture centred on x=0, because by symmetry the
black resultant vector (which is the value of the Fourier
transform at a particular θ) is horizontal – it is
always real. (If we chose one of the other vectors to be
always real – in other words we shifted the aperture to
one side, then the resultant vector would be the same
length, but it would also rotate in phase: this is the so-
called ‘shift theorem’ in Fourier-transform-theory-
speak.)
Okay. Now if you can picture how the resultant (black)
vector changes as the ‘snake’ of the red vectors gets
more and more tightly wound around, then you really can
do a Fourier transform in your head!
Thinking about it, the red vectors form part of the arc
of a circle. This total arc length remains constant at
all values of θ, but the radius of the circle gets
smaller and smaller as θ increases.
Lets just draw the sum of red vectors as a red line
(drawing lots of tiny red pointers is deadly dull). The
next diagram shows what happens to the red line and the
resultant black vector as θ increases:
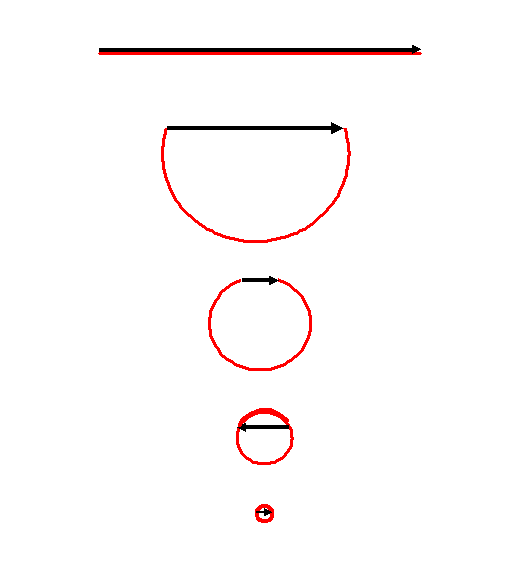
By the time we have reached the penultimate diagram, the
red circle has wrapped right over itself, and so the
resultant vector has changed sign. At higher and higher
values of θ the circle becomes even tighter,
wrapping around on itself over and over again, getting
smaller and smaller, with the resultant vector repeatedly
changing sign.
If we plot the resultant vector as a function of θ
this is what we can guess it will look like:
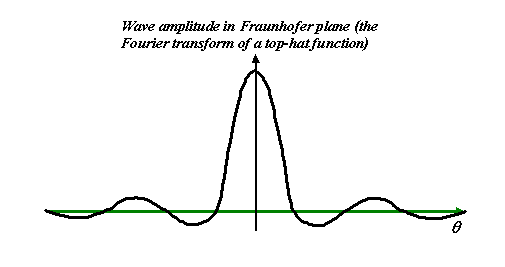
And indeed, this is exactly the Fourier transform of the
top-hat function. Because it crops up all over the place
in optics is has a special name: the sinc
function.
As a normal mortal electron microscopist, all you really
need to know about this function is its shape, the fact
as the aperture gets wider (‘a’ in the first diagram gets
larger) then the sinc function gets proportionally
narrower. (Such a simple fact can be used to give a
kinematical explanation of thickness fringes we see in
diffraction contrast.)
You can derive the formal mathematical expression for
this function easily by just doing the Fourier transform:
this is done in hundreds of textbooks. Here, I’m going
derive the same solution by using a geometric
construction from the folding-up circle.
The sinc function as a writhing snake:
The ‘writhing snake’ refers to the red circle above,
which slowly ties itself into a tight knot. What I want
to do is to work out the scattering amplitude (the length
of the black resultant vector in the diagrams above) as a
function of scattering angle, θ, using just simple
geometry.
The first thing to worry about is the total length of the
snake (the red line, made up of lots of little complex
vectors). Well, we worked out before that
at θ= 0, the Fourier transform is just the
integral of the whole function we are transforming. In
our case, because all the vectors are parallel (zero
phase) that means the entire length of snake is just 2aA.
Next, I want to worry about the radius of the circle made
by the writhing snake. To work this out, lets zoom into
a bit of the writhing snake, like this:
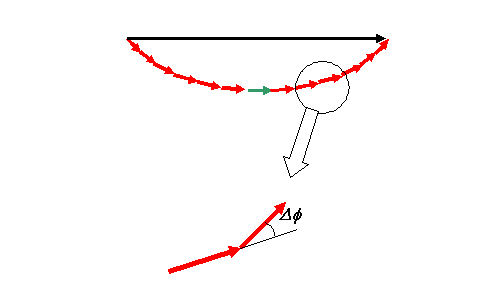
Here we are pretending the snake is made of discrete wave
amplitude vectors. In fact, we can let these tend to
having zero length, but it is easier to start like this.
Now Δφ is the phase angle introduced by phase
threads attached to adjacent bits of the wave function,
separated by a small distance, δx, like in the next
diagram.
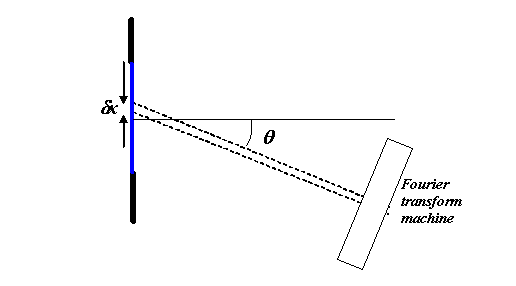
where have drawn our Fourier transform machine (see previous page). Clearly, Δφ is 2π
p/λ, where p = sinθ, but because as usual
we are only interested in small θ, then
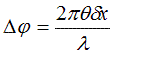
To make life simpler, I’m going get rid of all the
constants by putting
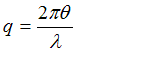
so that
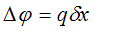
Going back to our red vectors, we have to find out the
length of each incremental bit of the snake. If the
total length of the snake is 2aA when x=2a, then the
length of the amplitude of wave corresponding to the
elemental bit δx is Aδx. We can use this to
work out the radius of circle of the writhing snake. For
very small δx, we can see from the following
diagram
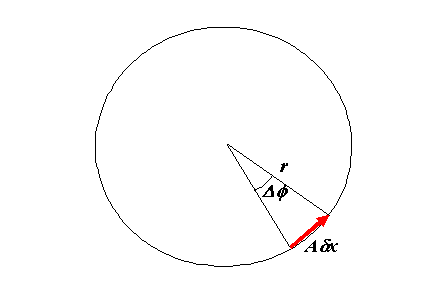
that the radius, r, is given by r=Aδx/Δφ.
So, substituting for Δφ, we have
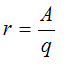
Now we know the radius of the circle and the length of
the snake, it’s easy to work out the resultant amplitude,
which I’ll call F. Look at the next diagram:
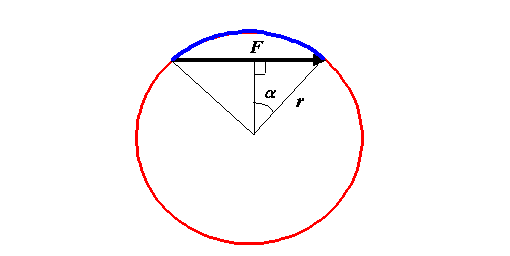
The resultant black vector is of length 2r sinα,
and 2α is just the length of blue arc divided by r.
The length of the blue arc is just the circumference of
the circle (2πr) minus the length of the whole snake, 2aA. That is to say
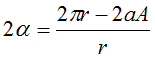
or
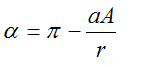
So, finally we can write:
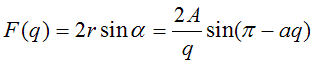
If we remember our elementary trig (I never can, but if
you sketch a sine curve you can work it out), then we
know that sin (π-aq)=sin(aq), so
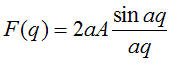
I’ve multiplied top and bottom by ‘a’, to emphasise that
sin aq is divided by aq. In the textbooks, you’ll see
this written with a further substitution, such that
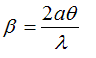
giving a final result (remembering our definition of q),
that
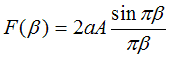
For a top hat function of unity height and width, this
reduces to sinπβ/πβ, which is the formal
definition of a sinc function. The sinc is just a sine
wave divided 1/(angle in the sine). The scaling of
β by π means that the function is zero whenever
β is an integer.
We can use the sinc function as a definition of the delta
function, which in turn can make the mathematical
manipulation of Fourier transforms, convolutions and
their inverses, very easy. The sinc function is
important in the scattering of waves from thin crystals
(as often encountered in electron microscopy), and crops
up in all sorts of other areas of space- and time-domain
analysis, in both optics, quantum mechanics, solid state
physics and even such fields as voice recognition.



Copyright J M Rodenburg
| 
