The Fourier Transform:
The Fraunhofer diffraction pattern (as opposed to the
Fresnel diffraction pattern) is mathematically identical
to the Fourier transform, at least within certain
approximations. We can therefore use our phase thread analogy to derive a pictorial
representation of the Fourier transform. Some non-
physicists are scared witless by the words ‘Fourier
transform’, which is used everywhere in the field of wave
optics. Unfortunately, it is really very hard to
understand electron microscopy without understanding the
Fourier transform.
On this page I hope to show that is easy to get a
picture in your mind’s eye of what’s happening: learning
to do Fourier transforms in your head is quite easy.
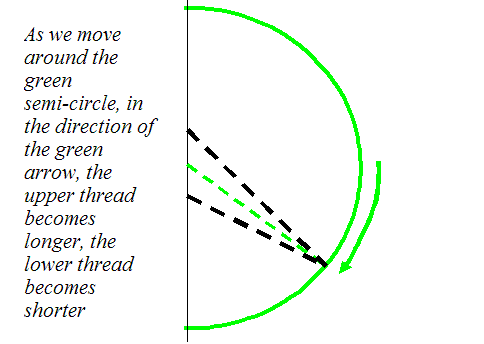
When we talked about our Young’s slits
experiment, we actually did a Fourier transform without
realising it. Remember, in order to calculate how two
waves would interfere with one another, we used a diagram
like this: .
If we wanted to represent our two slits
mathematically, we would draw a function like this: .
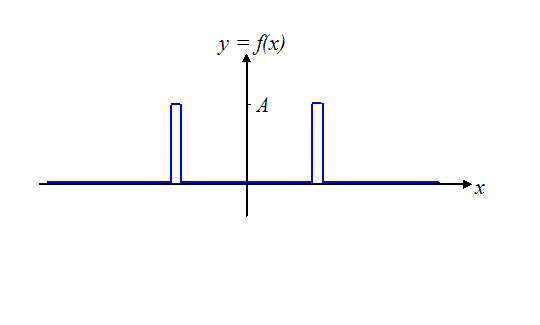
The function (in blue) is zero everywhere except at
the positions of the two slits where it has a value A
(imagine the spikes are very narrow): we can think of
this as the amplitude of the wave emanating from the
slit. (In general, the value of A can be complex, but
let’s assume it is real for the time being). I have been
careful to draw the slits equal distances either side of
the origin on the x-axis: this way the Fourier transform
is a purely real function. If you remember, with two
slits, a purely real function arrived over the green
curved surface in the far-field (Fraunhofer) diffraction
plane, and it looked like this: .
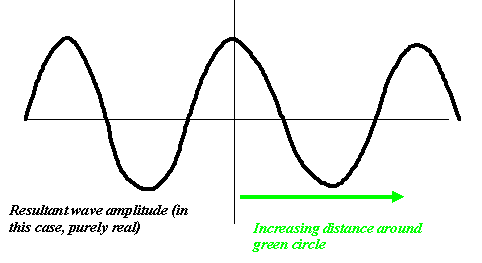
This wavy line function is the Fourier transform of
our original ‘two-spike’ function, shown above. Simple!
.
Before we go any further, lets just think what would
happen if we only had one slit, and it was positioned off-
axis, like this: .
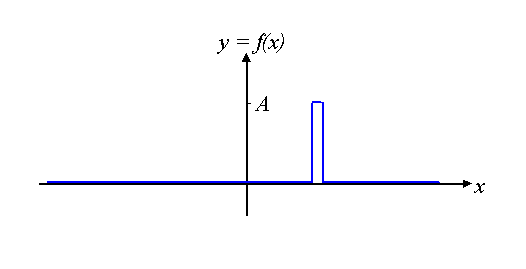
Well, remember how we constructed our Young’s slits
amplitude? If we only have one slit, only one phase
thread arrives in the far-field. Relative to the green
Gaussian surface we drew, a surface of constant phase of
the wave emanating from the single slit will look like
the blue line in the figure below: .
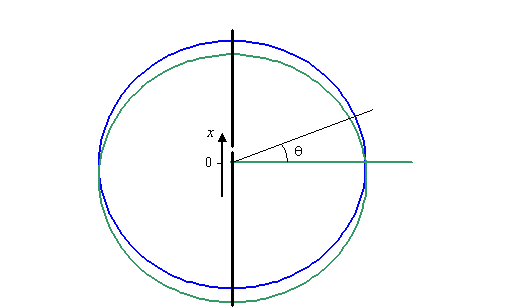
In the central region of the Fraunhofer diffraction
pattern, this blue line deviates from the green line as a
linear function of the scattering angle, θ. So if
we drew a graph of the path length difference between the
green and the blue line in the region of small θ,
the graph would look like this: .
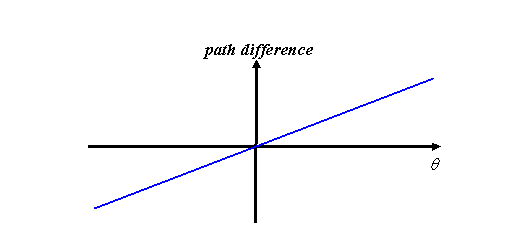
Now what does the complex value of the wave from this
slit look like? Well, there is only one thread
contributing to its value, and this is simply increasing
in phase constantly – in other words, it is itself a corkscrew function. Let’s plot the real part
of this corkscrew as a solid line, and the imaginary part
as a dotted line. As a function of θ, the angle
around the green circle, the Fourier transform of a
single (displaced) slit therefore looks like this: .
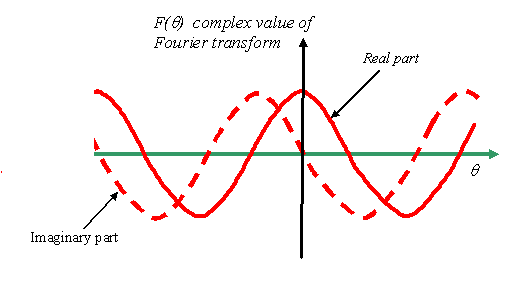
If we were to measure the intensity of this wave
distribution (which is all that we can do experimentally)
then it is a rather boring function which just has a
constant value, like this: .
Basically, because we only have one phase thread
involved, there is no other wave to interfere with it, so
all we are seeing is its constant amplitude (the length
of its complex vector) squared. However, the important
point I want to make here is that the underlying phase
(i.e. the complex value of the amplitude) of the wave
derived from an off-axis slit has a lot of structure in
it: it is a complex function. The Fourier transform of a
displaced spike is a corkscrew function. The more we
displace the spike (i.e. the slit), then across the green
Gaussian surface, this corkscrew has a higher and higher
frequency (as a function of θ, the phase of the
thread rotates more and more quickly).
This complex property of a Fourier transform is a
central cause of confusion amongst many students. People
are often taught that the Fourier transform of a spike
(called mathematically a delta function) is a
function of constant value. That’s true if the slit is
on the axis of the calculation (that is, positioned at
the centre of the green circle), but not if it is
shifted. This phase structure matters a great deal, say
if we consider how a lens would interact with the
Fraunhofer diffracted amplitude.
Okay, so what happens when we have a general function,
not just a spike or single slit? Well, there’re two
separate questions here. One is ‘how do we
mathematically define the Fourier transform?’ and the
other is ‘what is the scattered amplitude in the
Fraunhofer diffraction plane?’ Optics books will argue
that the complex value of a Fraunhofer (note: not
its intensity) is the Fourier transform of a wave being
scattered from an object. This is not very precise. Two
further questions arise. One is what it is we are taking
the Fourier transform of (is it the scattering object or the
wave that comes out of the scattering object), and the
other is the geometric approximation in which it is true
that the Fourier transform equals the Fraunhofer
diffraction pattern. In most electron microscopy
textbooks, these issues get mixed up. People talk of the
Fourier transform of the atomic potential and/or the
Fourier transform of an exit wavefield. The Ewald sphere
takes into account the geometric approximation in the
first case, the latter is used in the construction of the
Abbe theory of imaging (e.g. for calculating the bright-
field image or the contrast transfer function of the
objective lens).
Let’s tackle the geometric approximation first. The
Fraunhofer diffraction pattern exists, as we said before, when all the phase threads can be
thought of as being parallel to one another. For a very
large Gaussian surface (the green line in the first
diagram), and a relatively compact source of waves, this
condition is satisfied. However, for a single slit
displaced by a distance D from the centre of the Gaussian
surface, the path difference, p, as a function of θ
around the green circle is given by p = D sin θ.
Clearly, when θ= 90 degrees, the path difference for
the wave emanating from the displaced slit is just
exactly D: it can never get larger than this. However,
the mathematical definition of a Fourier transform relies
of the path difference p being exactly proportional to
θ (the coordinate of the Fraunhofer diffraction
plane). This is only true at small values of θ,
when sin θ is approximately equal to θ (when
θ is measured in radians). This small angle
approximation is always assumed as true in any electron
imaging situation (but not for Bragg diffraction at high
angles – we will discuss this later).
For the time being, we won’t worry about the
relationship between a scattering object and the wave it
produces, we’ll just worry about how some general wave
(usually over a two-dimensional surface) develops into a
Fraunhofer diffraction pattern, a very long way from its
source (and under the small scattering angle
approximation).
So, remember our harbour wall. Lets
now suppose that the wave disturbance within the harbour
wall is not the same everywhere between the walls (i.e.
we cannot represent it by an incident plane wave) but it
has some complex value: complex in both senses of the
word – a complicated structure in both modulus and phase.
We can draw such a function as before, using a solid line
to represent its real value and a dotted line to
represent its imaginary value. Here’s an example
function, which I will call f(x), plotted as a function
of x, the distance across the mouth of the harbour wall.
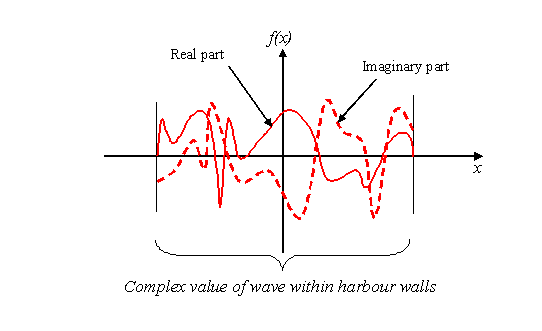
We now attach a phase thread to every
part of this function. As with our Young’s
slits experiment, each thread will be allowed to
propagate to a far off (green) Gaussian surface. We will
colour the thread coming from the centre of the harbour
wall as green: the phase of this thread is constant over
the entire Gaussian surface. The only important
difference between this experiment and Young’s slits
(apart from the very large number of phase threads, or
slits, that make up the total wave) is that each phase
thread has the modulus and phase (i.e. the complex value)
of the original wave (between the harbour walls) at the
point where it is attached to the wave. So, the phase
threads coming from the three points marked on our
example wave function –
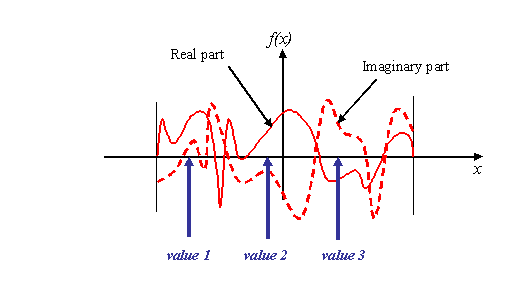
have the following respective complex values:
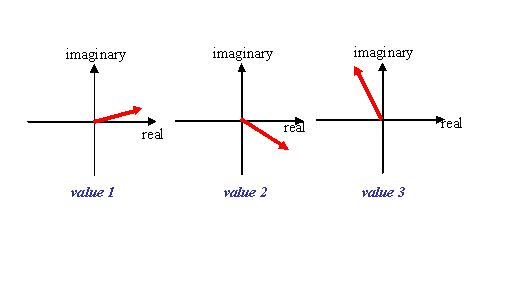
Remember, these are just the vector plots of the real
and imaginary parts of the value of the electron wave.
Now, at θ = 0, all the phase threads meet up on
the green surface. Because all the phase threads are
parallel (because the radius of the green circle is so
large), their total lengths are all identical, so when we
add them all together (because they all interfere with
one another) we just have to add together every real and
imaginary part of our original wave. That is, we
integrate (add up) every complex value of f(x). We write
this mathematically as:
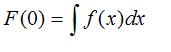
Where F(0) is the Fourier transform of f(x) at a value
of θ =0. So that’s easy. The value of a Fourier
transform of a function at 0 (in the Fourier transform
plane) is just the integral of the original function
(give or take a multiplicative factor which we will
discuss later). Remember, we have to add up all the
complex (real and imaginary) parts of f(x). The three
points in f(x) (values 1, 2 and 3) we discussed above add
to give a resultant (black vector) like this:
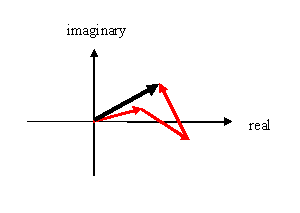
We have to add every other bit of f(x) together, which
will give some final complex vector, pointing off in some
direction. F(0) will (in general) be a complex number.
Now what about the Fourier transform at other values
θ?
To think this one through, imagine the mechanical
device shown below:
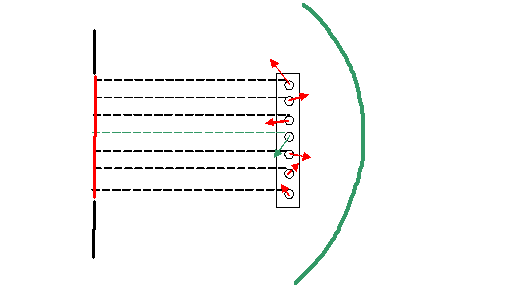
In this diagram, rather than thinking about millions
of threads (each coming from a tiny bit of f(x)), I’ve
just drawn seven threads, as if f(x) was made up of seven
slits (each of which is represented by a complex number).
The threads are wrapped around little wheels, each of
which has a circumference of exactly λ, the phase
thread (electron wave) wavelength.
Attached to the wheels are little wave values. To
calculate the Fourier transform at an angle θ, we
rotate the mechanical device around the green circle,
like this:
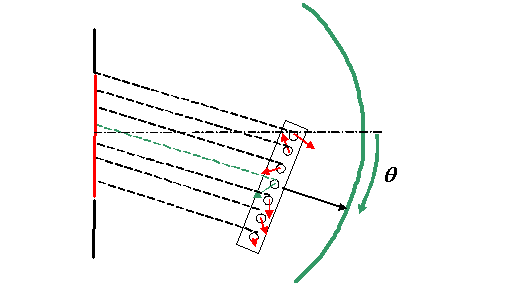
Of course, some phase threads get shorter, others get
longer, and, as they wrap around the wheels, their
associated wave values cycle around in phase. (We assume
the phase threads are kept taught). The Fourier
transform of the wave represented by f(x) is just the
addition of all these wave values (vectors) as a function
of θ.
We’ve already said that at θ =0, this integral
(the addition of the all the wave values) is just the
complex integral of the original function. At some angle
θ, we have to modify the phase of each bit of f(x)
(i.e. the length of its associate phase thread, and the
hence the phase angle of that particular bit of f(x))
before we do the integral.
How do we represent this mathematically?
Well, consider a bit of f(x) positioned at a distance
x = D, that is f(D), where D is a constant. At an angle
θ, the extra path length in the phase thread
associated with this bit of f(x) is p = D sin θ.
We’ve already said that we only interested in small
values of θ, so we can say approximately that p =
Dθ. The phase change in radians associated with
this extra path length is just 2πDθ/ λ.
So, the complex value of this phase thread is just f(D)
changed in phase by 2π p/λ. We could write
f(D) as the product of its modulus and phase, that is:
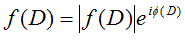
where φ(D) is the phase of f(D). The extra phase
change due to the extra length of phase at this
particular value of θ is added to this value. Call
the resultant complex wave value for this waved thread
W(D), then
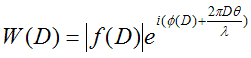
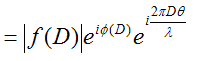
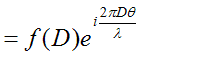
Of course, the same argument applies for all D=x, so
when we add up all the phase thread contributions, we
get
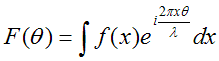
which is a mathematical formulation of both the
Fraunhofer diffraction amplitude and of the Fourier
transform.
Remember: to form a Fourier transform, we plot as a
function of angle θ the addition of all phase thread
values, taking into account their differences in path
length at a particular values of θ, where the phase
threads start off at θ= 0 with the modulus and phase
of the function we are Fourier transforming.
Of course, at θ=0, the exponential is unity,
giving simply the integral of f(x), as we saw above.
Okay, well we’ve made a few approximations here, both
from the point of view of the mathematics of a Fourier
transform and the actual diffracted amplitude in a real
scattering experiment, but the basic concept is correct.
From a mathematical point of view, it is most elegant
to define the Fourier transform as
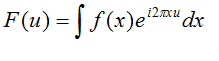
Here, the coordinate of the Fourier transform is u and
wavelength dependence (which is physical quantity, but
not a relevant mathematical quantity) has been dropped.
The beauty of this simpler definition is that the ‘back’
Fourier transform, that is the thing we do to F(u) to
work out f(x), is just
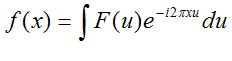
The back transform is identical to the forward
transform, except for a swapping of coordinates and the
minus sign in the exponential. Physically, you can think
of the back transform as reversing the direction of
travel of the waves back from the Fraunhofer pattern to
the object plane (harbour wall). Backward travelling
waves require the corkscrew (i.e. the sign of the
exponential) to be reversed.
In fact, physicists (and most electron microscopists)
leave the λ in the definition. If we also remember that 2π/λ is often called
k, then the Fourier transform is usually defined by
physicists as
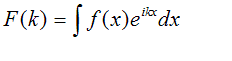
At first, this may seem the simplest definition so
far, because there are no constants in the exponential.
However, if you work through the integral, the back
transform now has to have a factor of 1/2π in front
of it to keep the magnitude scaling constant. (This is
because F(k) is ‘stretched out’ by a factor of 2π,
and so the inverse integral is 2π times larger,
because the area under the curve of F(k) is bigger by
this factor). For two-dimensional transforms, this
factor is squared (or raised to the power of N for N-
dimensional transforms). Some people define both the
forward and back transforms with a 1/(2π)
N/2 in front of the integral to keep the
apparent symmetry of the transforms. The forward
transform is also sometimes defined with the minus sign
in the exponential (in which case, the back transform has
a positive exponential). All these variants you can find
discussed in detail in the textbooks. The various
definitions have historically developed in different
fields of endeavour.



Copyright J M Rodenburg
| 
